בסרטון הזה נראה כיצד אפשר לסמן קבוצות מסוימות של מספרים ממשיים כקטעים על ציר המספרים. נערוך היכרות עם קטעים סגורים, קטעים פתוחים וקטעים חצי סגורים וחצי פתוחים.
צפה בסרטון
3
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
0
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
2.1-
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
3.02
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
1
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
2.17
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
קבוצה A וקבוצת המספרים הממשיים הן קבוצות שוות.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
קבוצה A היא תת-קבוצה של קבוצת המספרים הממשיים.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
קבוצת המספרים הממשיים היא תת-קבוצה של הקבוצה A.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
קבוצה A היא תת-קבוצה של קבוצת המספרים הראשוניים.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
קבוצת כל המספרים שבין 0 ל-3.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
קבוצת כל המספרים הממשיים.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
כל המספרים בין 6 ל-6- כפי שמסומן בציר המספרים.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$0leq x leq3$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$0prec xprec3$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
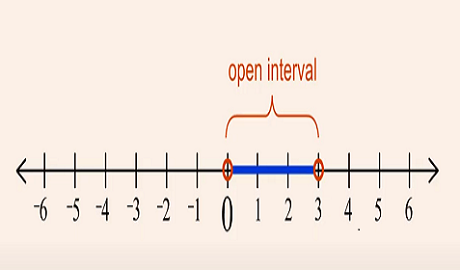
$0prec x$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$xprec3$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
בסרטון זה התלמידים ילמדו כיצד מקובל לסמן קטעים על ציר המספרים במספר אופנים, בין היתר באמצעות קטעים וסימונים מתמטיים שונים. השאלות מתבססות על הנאמר בסרטון. עם זאת, כדאי להגיע עם ידע קודם בתיאור קטעים באופן אלגברי וידע בסיסי בתורת הקבוצות, כגון תתי-קבוצות דיאגרמות ון. משך הסרטון כולל מענה על השאלות הוא כ-15 דק'.
אלגברה, תורת הקבוצות, סימון קטעים, אי שוויונות, דיאגרמות
הבניית ידע
בפעילות זו התלמידים ישתמשו בתוכנת דסמוס/גאוגברה כדי ליצור ציור מתמטי תוך כדי שימוש בפונקציות לינאריות (ניתן להרחיב לעוד סוגי פונקציות), ובתחומים מוגדרים כדי ליצור קטעים. לבסוף יקבלו תוצר של ציור כפי שיצרו. משימה זו יכולה להתבצע בזוגות ולשמש כהערכה חלופית.
מתמטיקה, אלגברה, תורת הקבוצות, סימון קטעים, אי שוויונות, פונקציות, קו ישר, שיפוע.
יישום ידע, יצירתיות, רפלקטיביות לתהליך הלמידה, שיתוף פעולה
בסרטון זה נלמד מדוע יתושים עוקצים? למה צריך להתגונן מפני עקיצות יתוש, ומה ניתן לעשות כדי להתמודד נגדם?
דניאל לוקח אותנו לטיול עירוני וחוקר אילו חיות בר מסתתרות לנו בין הבתים והעצים. הסרטון עונה על שאלות שונות ובין היתר מה הן חיות בר, ומהן הסיבות שאולי כדאי לא להאכיל אותן בסביבה עירונית.
