בסרטון הזה נראה מהם קטעים מנוונים, נכיר את תכונת הקשירות של קטעים ונראה איך אפשר לתאר קבוצות של מספרים ממשיים באמצעות איחוד של קטעים.
שלוש אפשרויות – סגורים משני צידיו, או פתוחים משני צידיו, או צד אחד פתוח וצד אחד סגור.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
אפשרות אחת – סגור משני צידיו. מכאן השם קטע חסום.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
שתי אפשרויות – סגורים משני צידיו או פתוחים משני צידיו.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
ארבע אפשרויות – סגורים משני צידיו, או פתוחים משני צידיו, או צד שמאל פתוח וצד ימין סגור, או צד שמאל סגור וצד ימין פתוח.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
זוהי קבוצה אין-סופית של מספרים, ומכאן הקטע מכיל את כל הנקודות שעל ציר המספרים.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
מצב כזה אינו מוגדר, ואי אפשר לכתוב זאת.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
זוהי קבוצה שמכילה נקודה אחת בלבד, ומכאן מספר ממשי אחד.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
זוהי קבוצה ריקה, ומכאן הקטע לא מכיל אף נקודה.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
רק מספרים חיוביים נכללים בקטע.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
רק מספרים שלמים נכללים בקטע.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
אף מספר ממשי לא נכלל בקטע.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
כל המספרים הממשיים נכללים בקטע.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
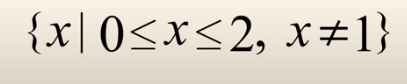
כן, אומנם ישנו מספר שאינו נכלל בקבוצה אך מכיוון שציינו זאת, אז הקבוצה הוצגה בעזרת קטע אחד.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
כן, כל מספר שנמצא בין 0 ל-2 נכלל בקבוצה, ולכן אפשר להציגו בעזרת קטע אחד.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
לא, ישנם מספרים רבים בין 0 ל-2 שאינם חלק מהקבוצה, ולכן נצטרך להציג קבוצה זו בעזרת קטעים רבים.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
לא, ישנו מספר בין 0 ל-2 שלא נכלל בקבוצה, ולכן אי אפשר להציגו בעזרת קטע אחד.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
בתורת הקבוצות – ובענפים אחרים במתמטיקה – האיחוד של אוסף של קבוצות הוא קבוצה שמכילה את כל מה ששייך לקבוצות אלה, ושום דבר אחר מלבד זה.
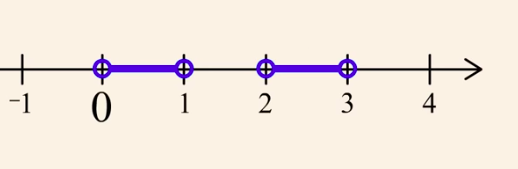
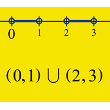
$(0,1)cap(2,3)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$(0,1)cup(2,3)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$(1,0)cup(3,2)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$(1,0)cap(3,2)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה

$left[-infty,0right]cupleft[0,inftyright]$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$(infty,0)cup(1,-infty)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$(infty,0)cup(0,infty)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$ (-infty,0)cup(0,infty)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$(-infty,0)cap(0,infty)$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
במקרים של האיחודים שראינו לשתי הקבוצות לא היו איברים משותפים. במקרה כזה הן מכונות "קבוצות זרות", ואיחודן מכונה "איחוד זר".
בסרטון זה התלמידים ילמדו על סוגי קטעים שונים. התלמידים יכירו את תכונת הקשירות של קטעים ונראה כיצד אפשר לתאר קבוצות של מספרים ממשיים באמצעות איחוד של קטעים. התלמידים יחשפו להגדרה של קטע ויישמו בהתאם מקרים שונים ואת אופן כתיבת איחוד קטעים ורישום קבוצות. אורך הסרטון כולל מענה על השאלות הינו כ- 15 דק'. בסיום הסרטון ישנו סיכום על הנאמר.
אלגברה, תורת הקבוצות, סימון קטעים, אי שוויונות, איחוד קטעים
הבניית ידע