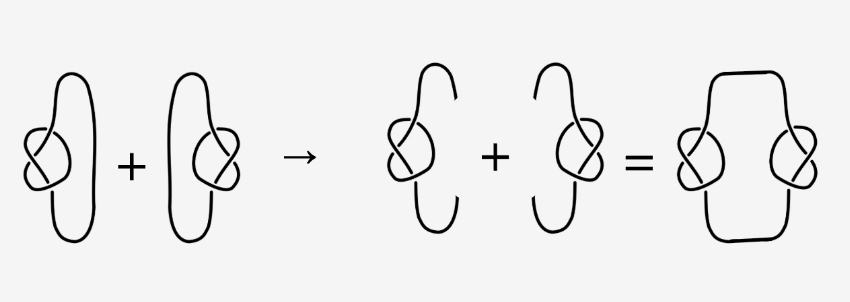הדוגמה שפרמה את הקשרים
שני מתמטיקאים מאוניברסיטת נברסקה הפריכו השערה מקובלת מאוד בתורת הקשרים. כל מה שהיו צריכים לשם כך היה דוגמה נגדית פשוטה

8 דצמבר 2025
|

5 דקות
|
גם בימינו, מתברר, אפשר לסתור השערות שמתמטיקאים רבים משוכנעים בלב שלם באמיתותן. זה מה שהראה מחקרם של המתמטיקאים מרק בריטנהם (Brittenham) וסוזן הרמילר (Hermiller), שהועלה לאחרונה לפרסום מקדים בארכיון מאמרים מתמטיים. החוקרים מפריכים השערה מתחום תורת הקשרים – ענף במתמטיקה שעוסק בקשרים ובדרכי התרתם. ההשתאות שעורר מחקרם נוגעת לא רק לתוכן המתמטי שלו, אלא בראש ובראשונה לכך שהם שברו קונספציה שהייתה מקובלת עשרות שנים.
זה קשר זה?
כדי להבין מה גילו בריטנהם והרמילר עלינו להבין קודם איך מתמטיקאים מתארים קשרים. כבר בשחר הימים החלו בני האדם לקשור קשרים, אבל רק במאתיים השנים האחרונות החלו מתמטיקאים לחקור קשרים באופן שיטתי.
כדי לפשט את התמונה, כשמתמטיקאים מתארים קשרים הם מדביקים את קצות החבל זה לזה. כך אי-אפשר להתיר קשר בלי לגזור קודם את החבל. אחד הקשרים הבסיסיים ביותר שקיימים הוא קשר הבוהן, שבו עושים בצד אחד של החבל טבעת קטנה ומכניסים לתוכה את הקצה הנגדי של החבל. מתמטיקאים מעדיפים לכנות אותו קשר תלת-עלעלי, או קשר תלתן. אפשר לצייר אותו בפשטות כקשר בחבל פתוח עם שני קצוות, או כשקצותיו מחוברים כנהוג בתורת הקשרים המתמטית.
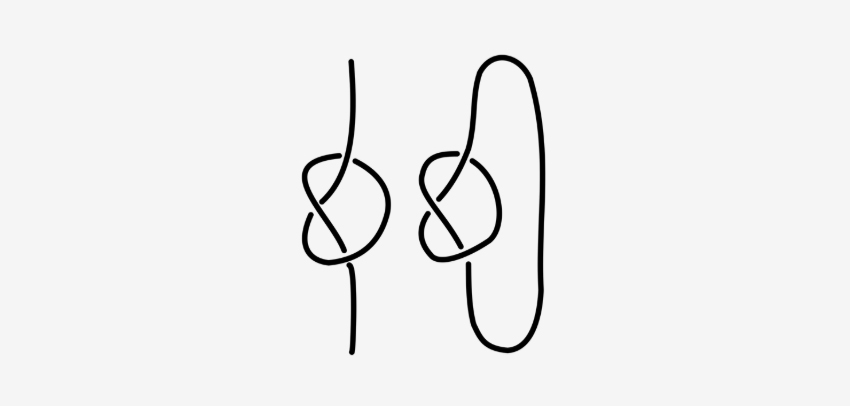
אחד הקשרים הבסיסיים ביותר שקיימים הוא קשר הבוהן. משמאל: קשר בוהן פתוח; מימין: התיאור המתמטי שלו. קשר מתמטי מתואר תמיד בתוך לולאה סגורה | איור: Talifero, מוויקיפדיה
רבים מתייחסים לקשר הבוהן בתור הקשר הפשוט ביותר, אבל יש קשר פשוט ממנו: הלולאה, או האל-קשר. מחקר מתמטי של קשרים הוא משימה מורכבת, בראש ובראשונה משום שקשה מאוד לסווג אותם. למשל,אם מסתכלים על הקשר מכיוונים שונים, הוא ייראה אחרת מכל כיוון. מספר הצמתים, כלומר המקומות שבהם החבל עובר מעל עצמו או ומתחת לעצמו, משתנה באותו קשר בהתאם לנקודת המבט של הצופה.

מחקר מתמטי של קשרים הוא משימה מורכבת, בראש ובראשונה משום שקשה מאוד לסווג אותם. שני הקשרים האלה הם אותו קשר מזוויות צפייה שונות | knotplot.com
גם עיוותים מסוימים עשויים לשנות את האופן שבו הקשר נראה, אך לא את הקשר עצמו. אם ניקח אל-קשר, למשל גומייה, ונסובב אותה בין שתי כפות הידיים. הגומייה תתעוות ותתלפף סביב עצמה, אבל מבחינה מתמטית לא נוצר בה שום קשר חדש. זו עדיין רק לולאה פשוטה. למעשה, כל קשר אפשר להציג באינסוף דרכים הצגות שונות.
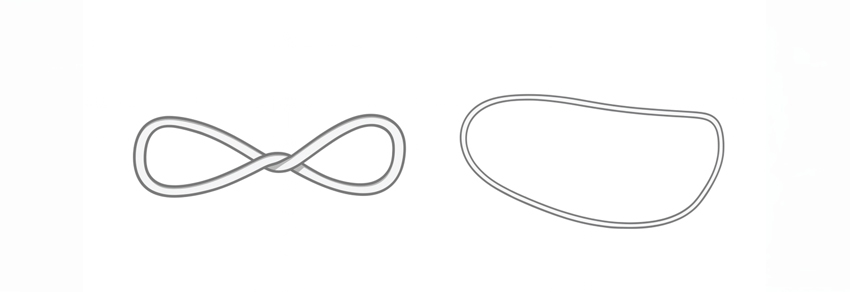
גם עיוותים מסוימים עשויים לשנות את האופן שבו הקשר נראה, אך לא את הקשר עצמו.שני הקשרים בתמונה זהים: מספיק לסובב אחת משתי הלולאות של הקשר השמאלי נגד כיוון הליפוף כדי להחזיר את הקשר לצורת לולאה פשוטה | knotplot.com
התרת הקשר
בואו נניח שיש לנו קשר. בכמה צעדים אפשר להתיר אותו לגמרי? איך בכלל אפשר להגדיר מתמטית מהי התרת קשר?
התבוננו לרגע בצומת אחד בקשר התלתן. דמיינו שאתם חותכים חבל שעובר מתחת לצומת, מעלים את שני הקצוות מעל הצומת ומדביקים אותם מחדש לחבל אחד רציף. הופ! הקשר נעלם. זוהי דוגמה להגדרה מתמטית של התרת הקשר.
בייצוג הפשוט ביותר של קשר תלתן יש שלושה צמתים, אבל די בכך שנעשה את התרגיל הזה בצומת אחד והקשר כולו יותר וייעלם. יתר על כן, אין קשר ברור בין מספר הצמתים בקשר לבין מספר הצעדים הדרושים כדי להתיר אותו לגמרי. לפעמים מספיק לעשות את זה בצומת אחד, ולפעמים יותר. מספר הצעדים הקטן ביותר האפשרי להתרת קשר בצורה הזאת נקרא “מספר התרת הקשר”.
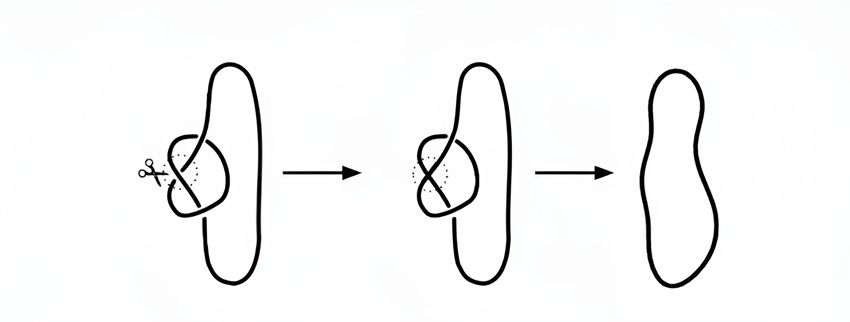
התרת קשר באופן מתמטי: מדמיינים שחותכים חבל שעובר מתחת לצומת, מעבירים את הקצוות מעל הצומת ומדביקים | יוסי אלרן
השאלה היא איך מזהים מהו מספר הקשר. מתמטיקאים ואנשי מדעי המחשב מתמודדים עם הבעיה הזאת כבר שנים רבות, ומתברר שזאת משימה לא פשוטה בכלל. אחת הסיבות לכך היא שצריך למצוא את הציור הנכון של הקשר – זה שיניב את מספר הצעדים הקטן ביותר. לפעמים דווקא הצורה המצוירת הפשוטה ביותר של קשר תוביל למספר התרת קשר שעולה על המספר המיטבי.
קשר ועוד קשר
לפני כמה החליטו בריטנהם והרמילר, מהמחלקה למתמטיקה באוניברסיטת נברסקה, להתעמק בהשערה מתמטית בת 88 שנה מתורת הקשרים. ההשערה קבעה שכשמחברים שני קשרים, מספר ההתרה של סכום הקשרים שווה לסכום מספרי ההתרה של כל קשר בנפרד.
חיבור קשרים הוא מנגנון שהגדירו מתמטיקאים עבור מקרה שבו יש לנו שני קשרים ואנחנו רוצים לחבר אותם. זה די פשוט ואינטואיטיבי: עלינו לחתוך כל אחד מהקשרים ולחבר את הקצוות של קשר אחד לאלה של השני, כדי ליצור קשר חדש שכולל את שניהם.
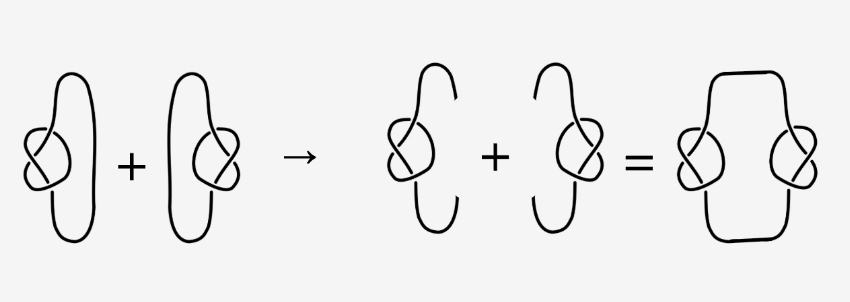
כדי לחבר שני קשרים, עלינו לחתוך כל אחד מהם ולחבר את הקצוות של קשר אחד לאלה של השני, כדי ליצור קשר חדש שכולל את שניהם. חיבור שני קשרי תלתן לקשר חדש | יוסי אלרן
ההשערה בדבר מספר ההתרה של סכום של שני קשרים נראתה הגיונית ופשוטה. אם להתרת קשר אחד דרושים x צעדים ולשני y צעדים, הגיוני להניח שהחיבור שלהם ידרוש x+y צעדים. כך חשבו גם הרבה מתמטיקאים, אך זו הייתה רק השערה, והשערות צריך להוכיח או להפריך. ובאמת, מתמטיקאים השקיעו שנים רבות בניסיונות מפרכים להוכיח את ההשערה.
ואז באו בריטנהם והרמילר והוכיחו שההשערה לא נכונה באמצעות דוגמה נגדית שסותרת אותה: הם מצאו שחיבור של קשר בעל שבעה צמתים, שמכונה 71, עם קשר נוסף שנראה כמו תמונת הראי שלו, מניב מספר התרה קטן מסכום מספרי ההתרה של כל קשר בנפרד. מספר התרת הקשר של הקשרים המקוריים הוא 3, כלומר דרושים שלושה צעדים כדי להתיר את כל הקשר. לעומת זאת, את הקשר המשותף הצליחו החוקרים להתיר בחמישה צעדים בלבד, כלומר מספר התרת הקשר שלו הוא 5 לכל היותר.
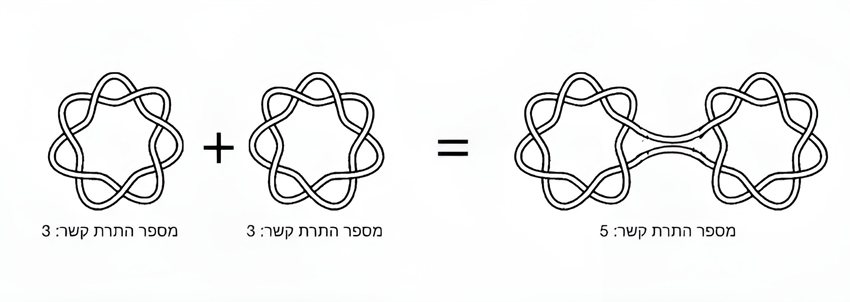
החיבור של קשר בעל שבעה צמתים עם קשר נוסף שנראה כמו תמונת הראי שלו, מניב מספר התרה קטן מסכום מספרי ההתרה של כל קשר בנפרד. הקשרים שנמצאו במחקר | Rolfsen Knot Table, עריכה: יוסי אלרן
חיבור שני הקשרים הללו, שמספר התרת הקשר של כל אחד מהם הוא 3, מניב קשר שמספר התרת הקשר שלו הוא 5, ולא 6, שהוא סכום מספרי התרת הקשר של שני הקשרים המקוריים יחד. כך הופרכה ההשערה.
החוקרים לא נפלו על הדוגמה במקרה. היה עליהם לפתח אלגוריתם – מערכת של כללים – לחישוב מספרי התרת קשר. אחרי התהליך המורכב הזה הם נדרשו לכתוב את התוכנה ולהפעיל אותה. כל זה דרש שעות מחשב רבות. אך ברגע שהמחשב פלט דוגמה אחת, ההשערה הופרכה.
המתמטיקאים העידו שכשהמחשב הודיע “סכום החיבורים נשבר” הם היו המומים. בדומה לרוב המתמטיקאים העוסקים בתורת הקשרים, גם הם סברו שההשערה נכונה. ראשית הם בדקו את התוכנה, מחשש שיתברר כי הממצא שלהם שגוי, מה גם שהקשר שהפריך את ההשערה לא היה מסובך במיוחד. הם אפילו בדקו עם חבל אמיתי שאכן אפשר להתיר את הקשר המחובר בחמישה צעדים בלבד. כשהצליחו הם נאלצו להודות: ההשערה הופרכה.
בריטנהם והרמילר פרסמו את תגליתם בארכיון המאמרים המתמטיים וקראו לעמיתיהם לבדוק אותם. הם גם הבהירו במאמר שחמש אינו בהכרח מספר ההתרה הסופי. בהחלט ייתכן שאפשר להתיר את הקשר אפילו בפחות צעדים, אם כי לא פחות משניים. עד מהרה הם מצאו עוד דוגמאות שמפריכות את ההשערה. אז מה הלקח? לפעמים קל יותר להתיר שני פלונטרים אם מחברים אותם יחד, במקום להתמודד עם כל אחד מהם בנפרד.